Boolean algebra and Logic Gates

Logic Gates and Boolean Algebra

Logic gates and Boolean algebra are fundamental concepts in digital electronics and computing. This guide will simplify these concepts and help you grasp the basics of logic gates and the operations of Boolean algebra.

Binary Digits: The Foundation of Computing

At the heart of digital computing is the binary system, which uses only two digits: 0 and 1. The digit 0 represents a low value, while 1 represents a high value. Every computer processes information using these binary digits. Understanding this binary philosophy is crucial for grasping more complex concepts in digital electronics.

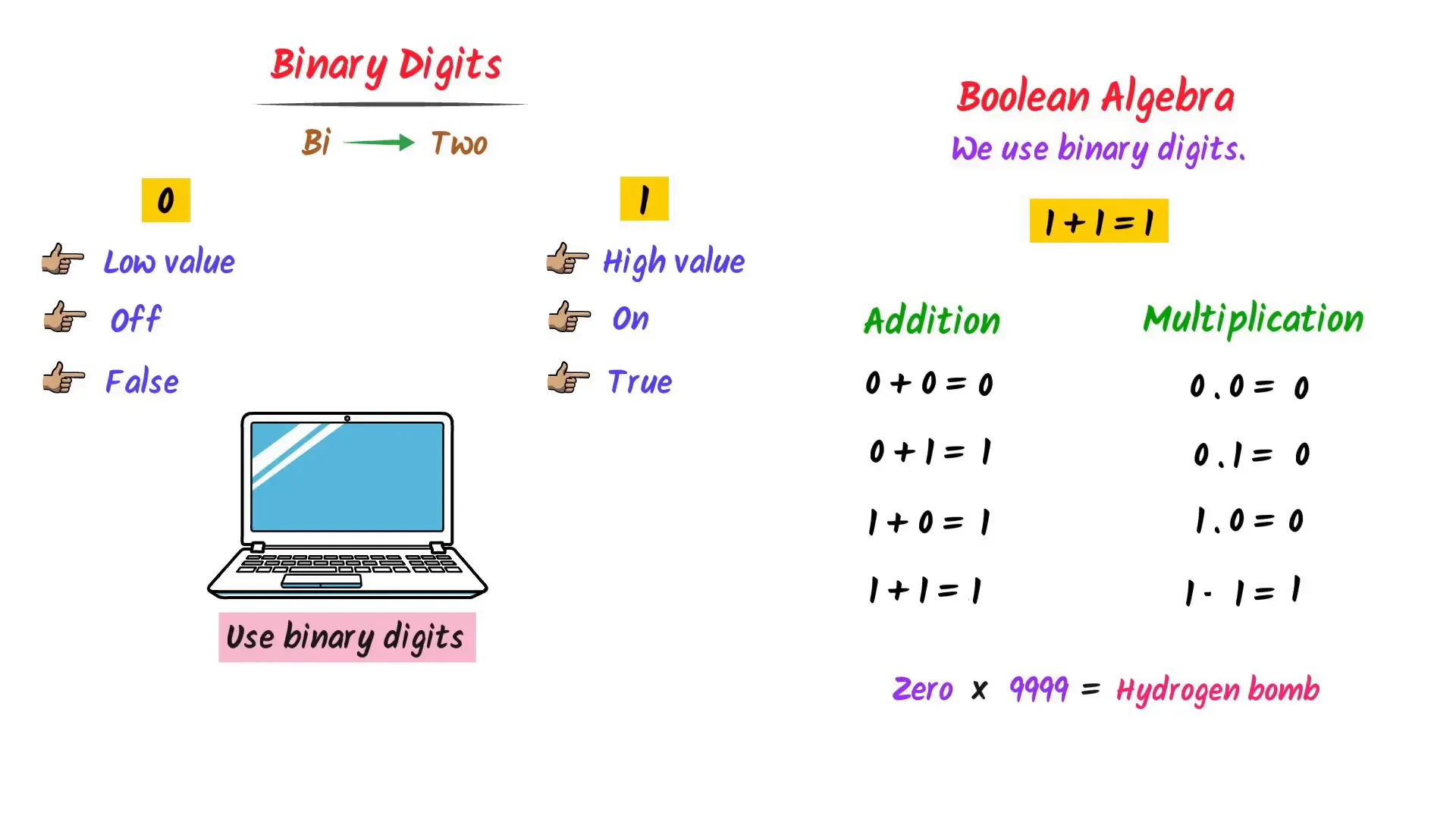
Introduction to Boolean Algebra

Boolean algebra is the mathematical framework that governs the operations of binary digits. A key principle of Boolean algebra is that 1 + 1 equals 1, as there are no digits beyond 1 in this system. This concept is essential when performing operations on binary digits.

Here are some basic operations in Boolean algebra:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 1

When it comes to multiplication:

• 0 * 0 = 0
• 0 * 1 = 0
• 1 * 0 = 0
• 1 * 1 = 1

In Boolean algebra, any operation involving 0 and multiplication results in 0, which is a crucial point to remember.

Inverse Values in Boolean Algebra

Every binary digit has an opposite, or inverse value. The inverse of 0 is 1, and the inverse of 1 is 0. This can be represented as follows:

• If A = 0, then A' (A bar) = 1
• If A = 1, then A' = 0

This relationship has significant implications when working with Boolean expressions. For instance, A + A' = 1, and A'' = A, meaning that inverting a value twice returns the original value.

Advanced Concepts in Boolean Algebra

A key theorem in Boolean algebra is:

(A + B)' = A'B'

This means that the inverse of the sum of two variables is equal to the product of their inverses. Understanding how to prove this can deepen your comprehension of Boolean algebra.

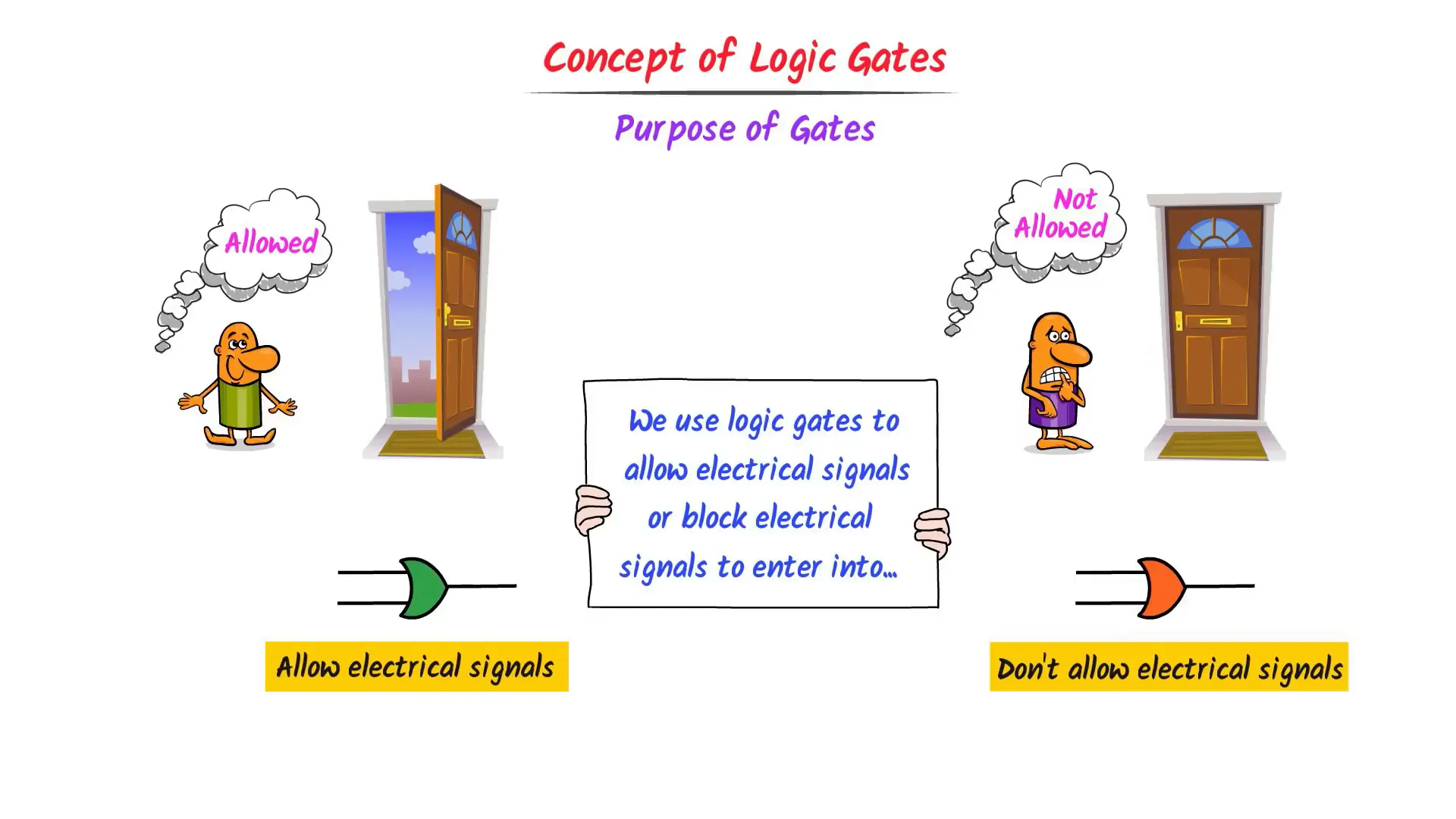
Introduction to Logic Gates

Logic gates are digital devices that perform Boolean functions. They take two inputs and provide one output, allowing or blocking electrical signals based on the operation defined by the gate. Understanding the basic purpose of these gates is essential for any digital circuit design.

Types of Basic Logic Gates

There are five fundamental types of logic gates: AND, OR, NOT, NOR, and NAND. Each gate performs a specific operation based on its inputs.

1. OR Gate

The OR gate adds its two inputs. The output Y is defined as:

Y = A + B

Here is the truth table for the OR gate:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 1

Here is the figure and Truth table for OR gate:

2. AND Gate

The AND gate multiplies its two inputs. The output Y is defined as:

Y = A · B

The truth table for the AND gate is as follows:

• 0 · 0 = 0
• 0 · 1 = 0
• 1 · 0 = 0
• 1 · 1 = 1

Here is the figure and Truth table for ANDgate:

3. NOT Gate

The NOT gate inverts its input. The output Y is defined as:

Y = A'

The truth table for the NOT gate is:

• If A = 1, then Y = 0
• If A = 0, then Y = 1

Here is the figure and Truth table for NOT gate:

4. NOR Gate

The NOR gate combines the functions of OR and NOT. It adds the inputs and then inverts the result:

Y = (A + B)' = A' · B'

The truth table for the NOR gate is:

• 0 + 0 = 1
• 0 + 1 = 0
• 1 + 0 = 0
• 1 + 1 = 0

Here is the figure and Truth table for NOR ( OR + NOT ) gate:

5. NAND Gate

The NAND gate combines the functions of AND and NOT. It multiplies the inputs and inverts the result:

Y = (A · B)' = A' + B'

The truth table for the NAND gate is:

• 0 · 0 = 1
• 0 · 1 = 1
• 1 · 0 = 1
• 1 · 1 = 0

Here is the figure and Truth table for NAND ( AND + NOT ) gate:

Writing Functions for Logic Gates

To write functions for any logic gate system, identify the type of gates and their connections. For example, with an AND gate followed by an OR gate:

• For inputs A and B to an AND gate: Y = A · B
• For C input to an OR gate: Y = A · B + C

This method can be applied to any logic gate system to derive the corresponding Boolean expression.

Conclusion

Understanding logic gates and Boolean algebra is essential for anyone interested in digital electronics. These concepts form the foundation of how computers process information, and mastering them can open doors to further exploration in the field of electronics and computing.