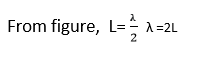Unit-3 Wave and Optics Notes
PDF Link:- View
Unit-3 Wave and Optics Notes
Organ pipe
A cylindrical hollow tube specially made fore produce musical sounds, of different harmonics by the vibration of air molecular into it is called an organ pipe. For example flute, whistle, etc.
Type of organ pipe
1. Closed organ pipe
2. Open organ pipe
1. Closed organ pipe
An organ pipe whose one end is closed and another is open is Called a closed organ pipe .for example bottle, cap of a pen, etc.

Fig: Closed organ pipe
When air is blown from the open end it gets reflected closed-end hence a stationary wave is produced at the closed end node is formed and at the open end anti-node is formed different types of modes of the mode of vibration of closed organ pipe are discussed below:
i. The fundamental mode of vibration
In the Fundamental mode of vibration of a closed organ pipe, one node is formed at the closed end and one anti-node is formed at the open end as shown in the figure below:

From figure
λ/4 [ ∴L=length of close organ pipe,λ=wave length of sound pipe]
= 4
If f0 is the frequency of the fundamental mode of vibration in a closed organ pipe then,

the first harmonic
ii. Second mode of vibration (first overtone)
In the second mode of vibration two-node and two anti-node are formed as shown in the figure below.

From figure,

IF f1 is the frequency of the second mode of vibration in a closed organ pipe then,

Hence, the frequency of the second mode of vibration is three times greater than the frequency of the fundamental mode of vibration in a closed organ pipe.
iii. The third mode of vibration (second overtone)
In the third mode of vibration three nodes and three antinodes are formed as the shown figure below

Fig: The third mode of Vibration
From the figure,

If f2 is the frequency of the third mode of vibration in a closed organ pipe then,

Hence, the frequency of the third mode of vibration is five times greater than the frequency of the fundamental mode of vibration in a closed pipe.
The Frequencies obtained as closed pipe are f0, 3f0, 5f0, ---
i.e Closed pipes give only odd harmonics
In general

Open Organ Pipe
An organ pipe whose both ends are open is called an open organ pipe. For eg:- Flute

When air is blown into the pipe through one end, a wave travels through the tube to the next and from where it is reflected. Hence a stationary wave is produced and at the open end, an anti-node is formed. The various modes of vibration in an open organ pipe are discussed below:
Modes of vibration in an open organ pipe are discussed below:
1. Fundamental mode of vibration

In the fundamental mode of vibration of the organ pipe, one node and two anti-nodes are formed, as shown in the figure above.
Let f0 be the frequency of the fundamental mode of vibration in an open organ pipe then,
ii. Second mode of vibration
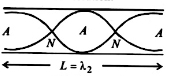
In the second vibration in an open organ pipe, two nodes, and two anti-nodes are formed as shown in the figure above,
From figure
L= λ
Let, f1 be the frequency of the second mode of vibration in an open organ pipe then,

Hence, the frequency of the second mode of vibration is twice time greater than the frequency of the fundamental mode of vibration in an open organ pipe.
iii. Third mode of vibration (Second Overtime)

In the third mode of vibration in an open organ pipe, 3 nodes of 4 anti-node are formed as shown in the figure above.
From figure:

Then,
Let F2 be the frequency of the third mode of vibration in an open organ pipe then,

Hence the frequency of the third mode of vibration is 3 times greater than the frequency of the fundamental mode of vibration in an open organ pipe
End correction
In an organ pipe, the air molecules at the open end are free to vibrate so that the wave extends a little into the air outside the pipe. The distance between the end point of the pipe and the position of the antinode formed outside the free end of the pipe is called end correction. It is denoted by 'e'.
End correction of closed pipe

from figure
L + e = λ/4
λ = 4(L + e)
End correction of open organ pipe

From figure
L+e+e = λ / 2
λ = 2(l+2e)
It is found that the end correction 'e' and internal diameter 'd' of a pipe are related as:
Wave in Strings
The velocity of the wave in a stretched string
Let us consider a transverse wave traveling along a string of length 'l' and mass 'm' with a velocity 'v' under tension 't' then it is found that the velocity of a wave depends upon
i) The tension 't' acting on String
i.e V α tˆa
ii) The mass 'm' acting on String
i.e V α mˆb
i) The length 'l' acting on String
i.e V α lˆe
Combining all
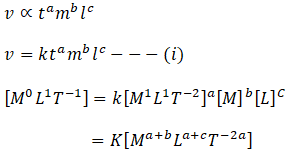
Comparing
a + b = 0 ---(i)
a + c = 1 ---(ii)
-2a = -1 ---(iii)
=> a = 1/2
=> a + b = 0
b = -1/2
=> a + c = 1
c = 1/2

Modes of vibration in a stretched string:
(1) First mode of vibration

In the first mode of vibration two nodes and one anti-nodes are formed as shown in the figure above. If ‘l’ be the length of string and ‘λ’ be the wavelength of the wave then from the figure,
![]()
If the frequency of the first mode of vibration is F1.

But,

This is a required relation for the first mode of vibration.
(2) Second mode of vibration

In the second mode of vibration, three nodes and two anti nodes are formed as shown in the figure above. If 'l' be the length 'λ' be the wavelength of string then,
from figure,
l = λ
The frequency of the second mode of vibration is f2.

But,

Hence the frequency of the second mode of vibration is 2 times greater than the frequency of the first mode of vibration
(3) The third mode of vibration

In the third mode of vibration 4 nodes and 3 anti-nodes are formed as shown in the figure above. If 'l' be the length of the string and 'λ' be the wavelength of the string then,
from figure,
L = 3λ / 2
2l / 3 = λ
The frequency of the third mode of vibration is f3.

Hence the frequency of the third mode of vibration is three times greater than the frequency of the first mode of vibration.
Resonance
When a body is capable of vibration or allowed to vibration freely, it will vibrate with its own frequency known as natural frequency. If the external period force is applied to a body then the body vibrates with the frequency of periodic force.
When the frequency of periodic force is equal to the natural frequency of the body then the amplitude of vibration is maximum. The phenomenon is called resonance.
The two conditions for occurring the resonance are:
1. The frequency of applied force must be equal to the natural frequency of the system
2. The applied force must be in phase with the vibrating system.
Resource tube experiment

Fig:- Resonance
where,
T=Tube
R=Reservoir
S=scale
The resonance tube consists of tube 'T' and reservoir 'R' which contains liquid. The tube and the reservoir are connected by a rubber tube and the scale 's' is attached to measure the air column in the tube. The length of the air column is adjusted by raising or lowering the label of liquid in the reservoir.
A vibrating tuning fork of non-frequency is placed over the mouth of tube 'T'. Hence this will vibrate by the air column inside the tube as shown in the figure above.
Initially when the label of water is lower down the frequency of vibration becomes equal to the natural frequency of the tuning fork and the first resonance occurs and a loud sound is produced.

Hence at the first resonance
![]()
Where l1 is the length of the air column inside the tube and ‘e’ be the end correction, also ‘λ’ be the wavelength.
When the label of liquid is further lowered down then second resonance is formed at another position of the tube

Hence at the second resonance,

Subtracting equation (i) from (ii)

If 'f' be the frequency of the tuning fork then the vibration of sound 'v'.

This gives the velocity of sound at room temperature
Suppose V and Vo be the velocity of sound.
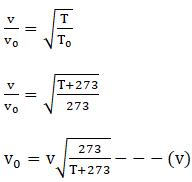
This gives the velocity of sound at 0℃
To determine end correction

Using Eqn (iii) in Eqn (vi)

Law of transverse vibration of a fixed stretched string
It can be stated as
1. Law of length
The frequency of transverse vibration of a stretched string is inversely proportional to its length 'l' when tension 'T' and mass per unit length 'μ' is constant.
i.e f α 1 / l for constant T and μ
2. Law of tension
The frequency of transverse vibration of a stretched string is directly proportional to square roots of tension 'T' when mass per unit length 'μ' and length 'l' is constant
i.e f α √T for constant length 'l' and μ
Law of mass per unit length
The frequency of transverse vibration of a stretched string is inversely proportional to square roots of mass per unit length 'mu' at constant tension 'T' and length 'l'
Verification of the laws of vibration of a fixed stretched string using a sonometer

The law of vibration occurs fixed stretched strings are verified by using a sonometer. It consists of a hollow wooden box with a wire fixed at its one end and stretched with the help of a load at the other end as shown in the figure above.
A vibrating tuning fork is placed vertically on the wooden box as shown in the figure and two bridges B1 and B2 are adjusted with their maximum vibration. The length between two bridges gives resonating length then the frequency of fundamental mode can be determined by using the formula,

(I). To verify the law of length [i.e. fα1/l]
To verify this, we take different tuning forks of known frequency and measure the resonating length for each of them by keeping constant tension ‘T’ and mass per unit length ‘u’ of wire.
If we plot a graph between f and 1/l a straight line passing through the origin can be formed as shown in the figure below.

(II). To verify the law of tension 'T' [ i.e f∝ √T]
To verify this, we observe resonance for the different tuning forks of different frequencies by varying tension on the string for the same resonating length of wire and its mass per unit length
If we plot a graph between f and √T, a straight line passing through the origin can be formed as shown in the figure below.
![To verify the law of tension 'T' [ i.e f∝ √T] To verify the law of tension 'T' [ i.e f∝ √T]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjuB28IX7Bh8D57ZZKcYgikSDqll770U-x63Bxfy5VxR9gYs0Jp1WzsaZf8xa3H3I7S0eyg6xzlX5IkH3yyZlgQBDbOtuiAeGjtSlqQKTnE0Wt7c7x0Sq9aLi3E7rCSJwn85ruLV3mu10Ie55MO7bEU4wdPKwijQ5ygLoSgD73KpVXdT2rzuG0pwWFB/s16000-rw/2.jpeg)
which verifies f∝ √T
(III). To verify the law of mass per unit length
To verify this we take a different tuning fork of different frequencies and observe the corresponding resonance for the different wires of different mass per unit length by keeping length 'l' and tension 'T' constant.
If we plot a graph between f∝ 1/√µ a straight line passing through the origin can be formed as shown in the figure below.

Which verifies f∝ 1/√µ