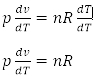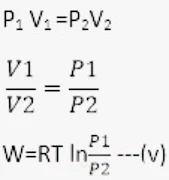chapter 4. First law of thermodynamics Notes

Unit-2 Heat and Thermodynamics

chapter 4. First law of thermodynamics Notes

PDF Link:- View

Downloading Update coming soon

 

Download PDF

Unit-2 Heat and Thermodynamics

chapter 4. First law of thermodynamics Notes

Thermodynamics System  

A Certain region in the space used to study the thermodynamic process is called a thermodynamics system. There are three types of thermodynamics Systems.

a) Open system

 The system which exchanges heat or matter is called an open system.

b) Closed System 

 The System which exchanges heat only is called a closed system.

c) Isolated System 

The System which exchanges neither heat and not matter is Called the Isolated system.

Thermodynamics Process

1) Isothermal Process

The process in which temperature remains constant is called the isothermal process.

We have, 

 PV = nRT 

for isothermal process PV = constant 

2) Isochoric process

The Process in which volume remains constant is called isochoric constant.

3) Isobaric process

The process in which pressure remains constant is called the isobaric process.

4) Adiabatic process

The process in which pressure, volume, and temperature change but the amount of heat remain constant is called the adiabatic process.

Work done by expansion

 Fig: Work done by expansion 

Let us consider a gas kept inside a cylinder provided with a movable and frictionless piston at pressure 'p', volume 'v', and temperature 'T'. Suppose the gas expands by a small volume 'dv' and the piston moved forward by distance  'dx'. If A is the cross-sectional area of the cylinder then force on the piston,

F = P.A       [∴ P=F/A]

Also, the change in volume

 dv = Adx

Now, 

Small work done,
dw= F.dx
dw= PAdx
dw= Pdv
which is external work done

PV diagram

The variation of pressure and volume in a thermodynamics process represented by the diagram is called the PV diagram. 

 

Area of KLJO = OJ x KO

= Pdv

= work done

Therefore, the area of the PV diagram gives the work done during the thermodynamics process. 

Internal energy

In the case of real gases, the molecules are attached to each other by intermolecular force and molecules are in motion. So, real gas molecules exhibit both potential energy and kinetic energy. Therefore, the sum of kinetic energy and potential energy is called internal energy. 

In the case of an ideal gas, there is no P.E. so in the case of ideal gas internal energy is K.E. only and depends upon absolute temperature.   

∴ Internal energy = kinetic energy + potential energy  

For Ideal gas, Internal energy = kinetic energy

First Law of thermodynamics

It states that if a certain amount of heat is supplied to the given system then a part of the heat may be used to increase the internal energy and the remaining part is used for work done.

If dQ is the amount of heat supplied to the system and du, dw is the increases in internal energy and external work done respectively, then according to the first law of thermodynamics.

dQ = du + dw --- (i)

since 

dQ = du + pdv

If dv = 0 then dw = 0

∴ dQ = du

It means the total amount of heat supplied is used to increase external work done only when the volume is constant.

Heat Capacity of gas

Molar heat as constant volume (Cv) 

It is defined as the amount of heat required to rise the temperature of 1 mole of gas through 1 kelvin at constant volume. It is denoted by Cv.

Molar heat as constant pressure (Cp)

It is defined as the amount of heat required to rise the temperature of 1 mole of gas through 1 kelvin at constant pressure. It is denoted by Cp.

Mayer's formula (Cp-Cv=R)

Fig: Gas in a cylinder

Let us consider 'n' mole of gas kept in a cylinder provided with the movable and frictionless piston at pressure 'P', volume 'V', and Temperature 'T'. Suppose the gas is heated at constant volume initially and dQ is the amount of heat given to the system to increase its temperature by dT then,

dQ = nCvdT --- (i)

From the first law of thermodynamics,

dQ = du + PdV 

Since, at constant volume, dv=0

 so, dQ = du

 ∴ du = nCv dT --- (ii)

 Again the gas is heated at constant pressure and dQ be the amount of heat given to the system to increase the temperature by dT.

dQ = nCpdT --- (iii)

 Again from first law of thermodynamics

 dQ = du + Pdv

 nCpdT = nCvdT + Pdv---(iv) ∴using equation (ii) 

 From idea gas equation

 PV = nRT

 Differentiating both sides with respect to at T at constant pressure.

Pdv = nRdT --- (v)

using eqn (v) in eqn (iv)

nCpdT = nCvdT + nRdT 

Cp = Cv+R 

Cp - Cv = R

Which is mayers formula

Equation of Adiabatic Process

From the first law of thermodynamics

dQ = du + pdv --- (i)

For adiabatic process

dQ = 0 (∴ heat constant)

du + Pdv = 0 --- (ii)

If Cv is the molar heat capacity at a constant volume for one mole of gas,

du = 1Cvdt --- (iii)

using equation (iii) in equation (ii)

CvdT +  Pdv = 0 --- (iv)

Also ideal gas equation for 1 mole of gas

PV = RT

Differentiating both sides with respect to 'T'

P dv / dT + V dP / dT = R dT / dT

P dv + vdP = R dT

dT = Pdv + Vdp / R --- (v)

using equation (v) in equation (iv)

Cv ( Pdv + Vdp / R ) + Pdv = 0

 Cv (Pdv + Vdp) + RPdv = 0

(CV+R) Pdv + CvVdp = 0   [ ∴ cp-cv=R]

CpPdv + CvVdp = 0 

Dividing both side by CvPv

Integrating on both sides 

Which is an adiabatic equation in terms of pressure and volume.

In terms of pressure and volume

In terms of temperature and volume

We have, 

PV=RT

Then equation (vi) becomes

In terms of pressure and temperature

We have,

Work done by an isothermal process 

Let us consider that 1 mole of gas is kept in a cylinder provided with a movable and frictionless piston. Also, let P1, V1, and T be the initial pressure, volume, and temperature respectively. By keeping the temperature constant volume can be changed to V2. So that pressure also changed to P2. So, that small work is done.

dw = PdV --- (i)

Thus total work done

for 1 mole of the gas ideal gas equation be,

PV = RT

P = RT / V --- (iii)

using equation (iii) in equation (ii)

 

Also from an isothermal process

Equations (iv) and (v) are required expressions for the isothermal process when gas is 1 mole

Work done by Adiabatic process 

Let us consider that 1 mole of gas is kept in a cylinder provided with a movable and frictionless piston. Also, Consider the gas expansion adiabatically from initial volume ‘V1’ to find volume ‘V2’.The work done is given by. 

using equation (ii) in (i)

For one mole of gas 

∴ PV=RT

 

Equations (iv) and (iii) are required expressions for n mole of gas during the adiabatic Process.

Reversible and Irreversible Process

The process which returns to the initial state from the final state exactly along the same path is called the reversible process. The net work done during the reversible process is O.

Fig: PV diagram for a reversible process

The process which doesn't return to the initial state from the final state exactly along the same path is called an irreversible process. The net work done during the irreversible process is net zero.

Fig: PV diagram for an irreversible process