Chapter 3. Fluid statics Notes

Unit-1 Mechanics

Chapter 3. Fluid statics Notes 

PDF Link:- View

Downloading Update coming soon

 

Download PDF

Unit-1 Mechanics

Chapter 3. Fluid statics Notes

Fluid

The substance which can flow from one point to another point is called fluid.

Example:- liquid and gas

Hydrostatics (fluid statics)

The study of fluid at rest is called hydrostatics.

Density

Mass per unit volume is called density. Its unit is kgm^-3

Relative density (specific gravity)

The relative density of a substance is the ratio of its density to the density of water at 4°C

Pressure

Force per unit area is called pressure. Its unit is N/m² or Pascal(pa)

In fluid pressure (p) = hdg

Derivation of Pressure in a liquid

Let us consider a liquid of density ‘ρ' Contained in a vessel of cross Sectional area ‘A’ up to height ‘h’ as shown in the figure.

Now,

Total mass of Liquid
(m) = volume (v) x density (ρ)

= Area(A) x height(h) x density(ρ)

= Ahρ

>Weight of Liquid is given by ;

W = mg

= Ahρg

So, The normal force on the bottom of the vessel is,

F = W

= Ahρθ

Finally,

The pressure by liquid at the bottom of the vessel is given by P=F/A

Ahρg / A

P= hρg

This is a required relation for pressure due to liquid and this relation shows that pressure due to liquid is directly proportional to

i)density of liquid

ii)height of liquid in the vessel

iii)Acceleration due to gravity at that place.

Principle of flotation

The principle of flotation states, "The weight of a floating body is equal to the weight of the liquid displaced". OR It states," A body is said to be floating in liquid if upthrust acting on the body is greater or equal to the weight of the body".

When a body is immersed in a liquid there are three cases

i ) When the weight of the body is greater than upthrust

Here, W > V

Vρg > Vρ₁g

∴ ρ >ρ₁

In this case, the body sinks and is set up at the bottom.

ii ) When the weight of the body is equal upthrust

Here, W = V

Vρg = Vρ₁g

∴ρ = ρ₁

In this case, the body lies inside a liquid with the upper surface on the surface of the liquid.

iii ) When the weight of the body is  less than upthrust

Here, W < V

Vρg < Vρ₁g

∴ρ <ρ₁

 In this case, a part of the body lies inside the liquid and the remaining part outside the liquid surface

The principle of floatation states that " A body is said to be in floating in liquid in upthrust acting on the body in greater or equal to the weight of the body.

Upthrust

The upward force by a fluid on an object which is completely or partially immersed in a fluid is called upthrust or buoyancy

Archimedes Principle

It states " When a body is fully or partially immersed in a fluid it expense an upthrust which is equal to the weight of the fluid displaced by the body."

i.e upthrust = weight of the fluid displaced

Pascals law

It states that " When pressure is applied to an enclosed liquid then the pressure is equally transmitted to every portion of it".

Centre of buoyancy

The center of gravity is the displaced liquid is called the center of buoyancy.

A floating body is said to be in equilibrium if the center of gravity and center of buoyancy of the body lies in the same vertical line

Surface Tension

Cohesive and adhesive force

The force of attraction between similar molecules is called cohesive force eg:- Force between water molecules.

The force of attraction between dissimilar molecules is called adhesive force eg:- Force between water and Glass molecules.

Surface Tension

The property by virtue of which liquid surface behaves like a stretched member and tends to occupy the minimum surface area is called surface tension.

Mathematically

Surface tension is the force per unit length of an imaginary line drawn in the plane of liquid surface action at the right angle of this line.

If 'f' be the force acting on the imaginary line of length 'l' then 

T= f/L

Note

a. In the case of an object 

i. when the object 'l' is on the surface of the liquid

T=f/l

ii. When an object of length 'L' is inside the liquid

T=F/2l

b. In case of a ring;

i. when a ring  of perimeter 2π on the surface of the liquid

T=F/2πR

ii) When a ring of '2πr' is inside the liquid;

c. In the case of a rectangle

i) When the rectangle of perimeter '2(l + b)' on the surface;

ii) When the rectangle of '2(l + b)' is inside the liquid;

Surface Energy

The amount of workdone against surface tension per unit change in surface area is called surface energy.

i.e.,

Let us consider a rectangle frame ABCD of wire in which BC can be slid horizontally. Suppose it is dipped in a soap solution such that a thin layer is deposited over an area. if BCD is due to surface tension (T) the layer tends to minimize surface area. Suppose, force 'F' is applied perpendicularly to BC towards outwards. So, the membrane is extended by a distance 'x' horizontally. Such that force is given by;

F = t.2l [ ∵ Since the soap film has two surfaces in contact with air, so total length of wire = 2l ]

So, workdone by this force 'F';

W = F x d

= F x X

W = t.2l.X

Hence,

This surface energy is equal to surface tension.

The shape of the Liquid Meniscus

i) Convex Meniscus

In the convex meniscus, the cohesive force between mercury molecules is greater than the adhesive force between mercury molecules and glass molecules.

i.e. FA < FC

ii) Concave Meniscus

In concave meniscus, the adhesive force between mercury molecules and water molecules is greater than the cohesive force between water molecules.

i.e. FA > FC

Angle of contact

The angle between the tangent to the liquid meniscus at the point of contact with the surface of solid inside the liquid surface is called the angle of contact. For example, The angle of contact for water glass is acute and the angle of contact for mercury glass is obtuse.

Capillarity

The phenomenon of rising or fan of the liquid in a capillary tube when dipped partially in it is called capillarity.

For example:

When a capillary tube with a narrow bore is dipped in water the level of water rise in the capillary tube.

When the same capillary tube is dipped in mercury the level of liquid in a capillary tube.

Measurement of Surface tension by capillary rise tube

Let us consider a capillary tube of radius 'r' is dipped in a liquid of density 'የ'. Let 'h' be the height above which liquid rise in the capillary tube. The surface tension acting tangentially at the concave meniscus is equal and opposite to the relation i.e. T = R. If 'θ' be the angle of contact, then 'T' can be resolved into two components Tsinθ along horizontal and Tcosθ along vertical. The horizontal components cancel each other and the vertical components add up together which pulls liquid upwards.

The total vertical force acting upward throughout the circumference is given by;

F = Tcosθ.2πr --- (i)

This force pulls the liquid upwards until the weight of the rising liquid equals upward force.

Now, the volume of liquid in the tube above the free surface of the liquid is given by;

V = [Volume of cylinder of radius 'r' and height 'h'] + [Volume of cylinder of radius 'r' and height 'h'] - [Volume of hemisphere of radius 'r']

So, the Weight of light rise;

W = mass of light x g

At equilibrium;

Total upward force = Weight of liquid rise;

Thus, knowing r,h,θ,የ, and g value, T can be calculated.

For narrow tubes;

Viscosity

The property virtue by which a fluid layer opposes the relative motion of its different layer is called viscosity.

Generally,

Viscosity means the frictional force acting between the layers of fluid that oppose the relative motion between them.

Newton's formula for viscosity

Fig: Different layers of liquid flowing over the solid surface

Let us consider a liquid flowing over the fixed solid horizontal surface. The liquid flow in different layers is parallel to the fixed surface. The layer in contact with the fixed surface is at rest while the velocity of the other layer increases uniformly upward

Let 'A' be the area of layers in contact and v and v+du are the velocity of the layer at distance x and x+dx from fixed surface respectively then dv/dx is the velocity gradient.

Then, according to Newton's law of viscosity, viscus force 'F' acting between two layers of liquid is

i) directly proportional to the area of contact

i.e;  F∝A---(i)

And,

ii) directly proportional to velocity gradient;

Combining equation (i) and (ii), Then;

where 'η' is the proportionality constant called the coefficient of Viscosity. The negative sign indicates viscous force decrease the relative motion/velocity between two layers

 

Thus, the coefficient of viscosity is defined as the viscous force acting per unit area having a unit velocity gradient.

Q) Find the dimensional formula of the coefficient of viscosity?

solution

Poiseuille's Formula

Fig: Streamline the flow of liquid in a capillary tube.

Poiseuillie concluded that the volume 'V' of the liquid flowing per second through a capillary tube is;

i) directly proportional to the pressure difference between two ends;

ii) directly proportional to the fourth power of the radius of the tube;

iii) Inversely proportional to the coefficient of viscosity of liquid;

iv) Inversely proportional to the length of the capillary tube;

Combining equation (i),(ii),(iii)and(iv); we get;

 

Where k= π/8 is called proportionality constant.

This is called Poiseuille's formula.

Derivation of Poiseuillie's Formula by a dimensional method

Solution

Consider a liquid through a capillary tube of radius r with length 'l' such that the pressure difference between the two ends of the tube is;

According to Poiseuillies;

The volume per second 'v' depends upon;

i) The pressure gradient (p/l)

ii) Radius of Capillary tube (r)

iii) Coefficient of Viscosity(η)

In dimensional form;

Where k = π/8 is called proportionality constant.

The dimensional equation (i) is ;

Equating dimension;

a + c = 0---(i)

-2b + b - c = 3 ---(ii)

-2a - c = -1
a + a + c = 1
a = 1 from(i)

Then (i) become;
c = 0-1
c = -1

Also, (ii) becomes;
-2 + b + 1 = 3
b = 4

Putting, a = 1, b = 4, c = 1 and then equation (i) becomes;

Which is Poiseuillies formula

Stoke's Law

When a spherical body falls through the liquid, the upthrust and viscous force acting upward direction and weight of the body act in a downward direction with an increase in velocity of the body the viscous forces equal to the downward force of the body falling with constant velocity is called terminal velocity.

Stroke's law found that the viscous force(F) acting on a spherical body of radius 'r' moving with terminal velocity 'v' in a fluid of coefficient of viscosity 'η' is;

F = 6πηrv

Derivation of Stoke's law by dimensional method

Consider a spherical body of radius 'r' falling through a liquid of coefficient of viscosity(η) with terminal velocity 'v'. Then,

According to Stoke's.

Viscous force(F) depends upon 

i) Coefficient of viscosity(η)

ii) Terminal velocity of the body(v)

iii) Radius of Spherical body (r)

Then,

In Dimensional Form;

Where k is proportionality constant = 6⊼

The dimensional equation of equation (i) is;

Equating dimensions of both sides;

a = 1

-a-b=-2
1+b=2
b=1

-a-b+c=1
-1+1+c=1
c=1

putting a = 1, b = 1, c = 1 in equation (i), we get,

This is Stoke's law

Measurement of Coefficient of Viscosity by using stoke's Law

Fig: Sphere falling into a liquid

Let us consider a sphere of radius 'r' and density 'ρ' falling through a liquid of density 's' with terminal velocity 'v'. In this case, the force acting on a body is

i. Weight of sphere (W) =

ii. Upthrust (v) = weight of liquid displaced

iii. Viscous force (f) = 6πηrv

Where η is the coefficient of viscosity

When the speed of the body in a downward direction increases the viscous force also increases and at a certain time the upward force acting on the body equals to downward force and the body attains equilibrium;

This is a required expression for the coefficient of viscosity

Bernoulli's Theorem

Bernoulli's theorem states, " For the stream-line flow of an ideal liquid (non - viscous and incompressible), the total energy (the sum of PE, KE, and Pressure energy) per unit mass remains constant at every cross-section throughout the flow".

Fig: Bernoulli's theorem

Let us consider a pipe AB in which non-viscous and compressible fluid is flowing. Let a1, p1, v1, h1 and a2, p2, v2, and h2 be the area of crosssection pressure velocity and height at end A and B respectively. Also, let; in time 'Δt' the fluid at end A reach to A' and at end B' reach to B.

Now;

Force acting on the fluid at end A, F1 = p1a1

∴Workdone on the fluid at end A;

W1 = (p1 x a1) . (v1 x Δt) [∵F1 = p1 a1 and V = d / t]

Similarly,

Workdone by fluid at end B' to B;

W2 = a2.q2.v2 at

Thus, Net work done on the fluid from moving A to B be;

From the equation of continuity;

Then from(i)

Let 'm' be the mass of liquid flowing through the pipe in 'Δt' then change in K.E;

Similarly;

Change in P.E ;

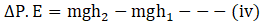
Now,

Total work done = Total change in energy;

Divide by 'ρ' into both sides 

Equation of continuity

Fig: Steady flow of liquid

Let us consider a liquid flowing through a pipe of cross-sectional area 'a1' and 'a2' at the left end respectively. Also let, v1,ρ1, and v2,ρ2 are the velocities and density of the liquid at their respective end. Now, the volume per second of liquid enters the pipe at the left end.

Again, the Mass of liquid entering per second at the left end ;

Similarly; the mass of liquid per second at the right end;

If there is no loss of liquid in the tube then;

Also, If the liquid is incompressible then,

This is called an equation of continuity

This is called stated that if the area of cross-section of the tube becomes larger then liquids speed becomes similar and vice-versa