Unit-1 Mechanics
Chapter 1 Rotational Dynamic
Moment of inertia of a rotating body
The inability of a body to change its state of rest or state of uniform rotational motion by itself or the inertia of a body in rotational motion is called rotational inertia or moment of inertia.
Let us consider a rigid body that consists of particles of masses m1, m2, m3 --- mn with distance r1, r2, r3 --- rn from the axis of rotational AB. The moment of inertia of the body about axis AB is defined by,


Thus, a moment of inertia of a rigid body is defined as the sum of the product of mass and the square of the distance from the axis of rotation of individual particles.
Moment of inertia of the uniform rod
1) About the axis passing through the center and perpendicular to its length
Let us consider a uniform rod of length 'l' and mass 'm'. Let AB be the axis passing through the center and perpendicular to its length about which moment of inertia is to be determined.

Fig: Moment of inertia of the uniform rod
consider a small segment of length ‘dx’ at a distance 'x' from one end as shown in figure center.
Now mass per unit length of the rod = m / l.
So, mass of the small segment (dx) = (m / l) . dx
Now, a moment of inertia of a small segment about axis AB,

Thus, a moment of inertia of the whole rod about axis AB is obtained by integrating equation (i) as,

This is a required expression for M.I of a uniform rod when the axis passes through the center and is perpendicular to its length.
2. About the axis passing through one end and perpendicular to the length.
Let us consider a uniform rod of length 'l' and mass 'm'. Let AB be the axis passing through one end and perpendicular to its length about which momentum intertie is to be determined.

consider a small segment of length 'dx' at distance 'x' from one end as shown in the figure;
Now, mass per unit length of the rod = m/l
so, mass of segment (dx) = m/l.dx
Now, the moment of inertia of a small segment about axis AB,

Thus, a moment of inertia of the whose rod about the axis of AB is obtained by integrating equation (i) as


This is a required expression for 'I' of a uniform rod when the axis passes through one end perpendicular to its length.
Kinetic Energy of Rotating Body
Let us consider a rigid body that consists of particles of masses m1,m2,.., mn with distances r1,r2,…., from the axis of rotation AB. Also, let w be the angular velocity with which it is rotating and v1,v2,…. vn be the linear velocity of respective particles m1,m2,…., mn

Fig: A rigid body rotating

Similarly, rotational K.E of other particles can be written as,

So, Rotational K.E of whole body = Sum of K.E of individual particles
Rotational K.E = T1 + T2 + T3 + ---- + Tn

So, the rotational K.E of a body is equal to half of the product of the momentum of inertia of the body and the square of the angular velocity of the body about the given axis of rotation.
The torque acting on rigid body
Let us consider a rigid body that consists of particles of masses m1, m2, m3, --- mn, with distance r1, r2, r3 --- rn from the axis of rotation AB. Suppose torque (T) is applied to the body which produces angular acceleration (α) on the body. Let F1, F2,… Fn are the forces acting on individual particles producing acceleration a1, a2, ... a such that a1 = r1 α a2 = r2 α --- an = rn α

Now, the force acting on the first particles,
F1 = m1 a1
= m1 r1α
Again,
Torque acting on this particle about axis of rotation,
T1 = r1 F1
= r1 m1 r1
= m1 r1^2α
Similarly, Torque acting on other particles,
T2 = m2 r2^2α, T3 = m3 r3^2α ,... Tn = mn rn^2α
Thus,
Now torque on the whole body = Sum of individual torque

This is the relation between the moment of inertia of a body and torque.
Angular momentum
The moment of linear momentum of an object is called angular momentum. It is denoted by 'L' and given by
.png)
Fig: Angular momentum of a particle
L = linear momentum X perpendicular distance from the axis of rotation
L = mvr ---(i)
since v = ωrL = m(ωr)r

Equations (i) and (ii) is an expressions for angular momentum. It is a vector quantity and its unit is

Angular momentum
Let us consider a rigid body that consists of particles of masses m1,m2,m3,.......mn with distance r1,r2,r3.......rn from the axis of rotation AB. Also let the body be rotating with angular velocity 'ω' and v1,v2,v3,..... vn be the linear velocities of respective particles m1,m2,m3,.....mn then,



This is the required relation between angular momentum and the moment of inertia of a body which shows that the magnitude of angular momentum of a body about a given axis is equal to the product of the moment of inertia ‘I’ of the body and its angular velocity ‘w ‘ about that axis.
Relation between angular momentum and torque
We have, the angular momentum (L) of a rigid body rotating about an axis with angular velocity ‘w’ is
L = IW --- (i)
Where, I = Moment of inertial of a body
different equation (i) with respect to time, we get

where α = dw / dt = angular acceleration
Also,
torque on the body is,
τ = Iα --- (iii)
comparing equations (ii) and (iii) we get
τ = dL / dt
This is the required relation between torque and angular momentum and this relation shows that torque acting on a body is equal to the rate of change of angular momentum of the body.
Principle of Conservation of Angular Momentum
It states that " If no external torques act on the system then total angular momentum remains constant."
i.e If τ = 0 then,
L = Constant
IW = constant
In gernal I1W1 = I2W2
proof
Since torque acting on a body is equal to the rate of change of angular momentum.
i.e. τ = dL/dt
If τ = 0 then,
dL/dt = 0
dL = 0
On integrating, we get
L= constant
IW = constant
In general I1W1 = I2W2
This proves the principle of conservation of angular momentum.
Work done by a couple and power in rotational motion
Let us consider, that a wheel is to be acted upon by a couple of forces ( F, F ) at points A and B. Let the wheel turns through angle 'θ' in a time 'dt' such that points A and B are displaced to points A' and B' and let 'S' be the linear displacement.
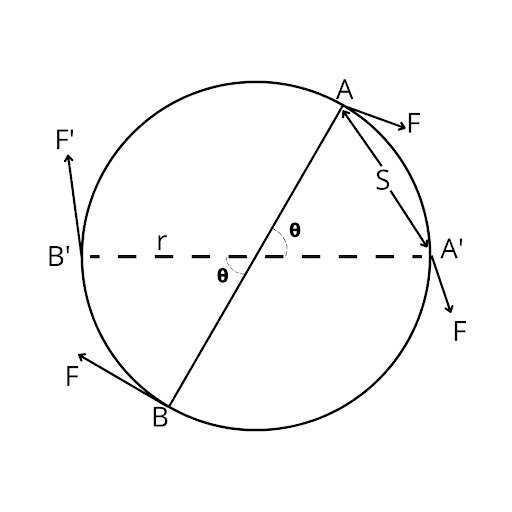
Fig: Work done by the torque
Now, workdone by force at point A,
WA = F.S
Also, the workdone by force at point B,
WB = F.S
∵ Total work done (W) = WA + WB
= F.S +F.S
= 2FS ---(i)
Also, from the figure,

∵ Work done (w) = 2 fθr
= (f.2r)θ
= τθ [ ∵ f.2r is the torque due to couple ]
so, work done by a couple (w) = τθ
Thus, work done by a couple is the product of torque and the angle of rotation of the rigid body.
Again,

Radius of Gyration
The perpendicular distance between the center of mass and the axis of rotation of a rigid body is called the radius of gyration. If 'm' is the mass of the body and k is its radius of gyration, then the moment of inertia of the body is given by,










